Pattern recognition assignment—CRF
Published:
模式识别课程作业—CRF
问题描述
给定左侧19条序列和右侧任务(已知yi-1=N, xi=1, 求解yi),证明CRF的推断结果为D

Solution
1. 简化问题 && 约定
- 约定Tag集合 S = {N,V,P,V}, 单词集合 T = {a,c}
# S,T集合
setS = ('D','N','P','V')
setT = ('a','c')
- 约定语句向量长度为3(即Tag1 -> Tag2 -> word1),并且我们只需要推断长度为3的语句
- ydot 集合由训练集合中没有出现的语句向量所构成
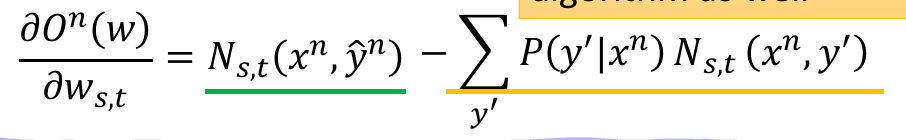
2. Feature Vector
- 由于我们要推断的序列长度为3, 因此要推断的目标序列只有如下四个
# 构造目标特征序列
objSeqList = ["NVa","NDa","NPa","NNa"]
- 构造特征feature的时候,参考课件中的
Feature Vector的两个部分part1= relations between tags and words,part2= relations between tags,这样会得到相当高维度的向量,很多分量的值为,因此可以将其剔除,最终只需要构造1x4的特征向量
def getFai(objSeq,seq):
# 加上 start and end,分别标定为0,1
objSeq = '0' + objSeq + '1'
seq = '0' + seq + '1'
fai = np.zeros((len(objSeq)-1),dtype=np.int16)
for i in range(len(objSeq)-1):
for j in range(len(seq)-1):
if objSeq[i] == seq[i] and objSeq[i+1] == seq[i+1]:
fai[i] = fai[i] + 1
return fai
3. Training
- Gradient Ascent
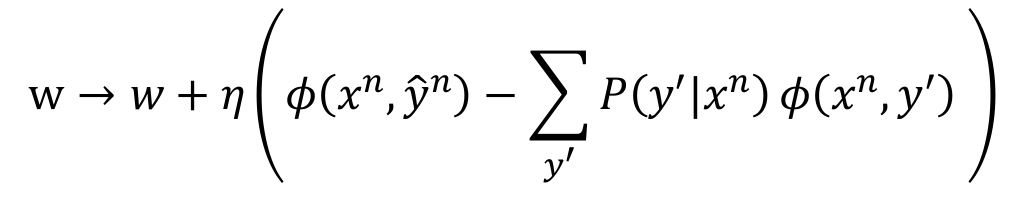
def Train(objSeq,eta,e,times):
# generate W randomly
W = np.random.rand(len(objSeq)+1)
for i in range(times):
for seq in trainingData:
dOW = getFai(objSeq,seq) - getSum(objSeq[-1],W,objSeq)
if abs(dOW).all() < e:
return W
W = W + eta*(dOW)
return W
4. Inference
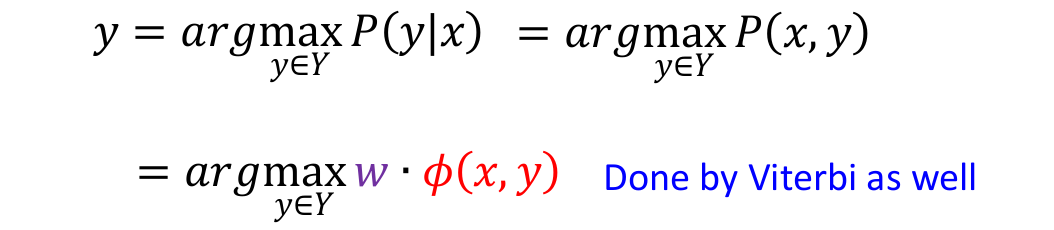
if __name__ == '__main__':
maxWi,maxPi,maxSeq = np.ones((len(objSeqList[0])+1)),0,0
# 遍历所有目标序列,计算联合概率
np.set_printoptions(formatter={'float': '{: 0.8f}'.format})
for objSeq in objSeqList:
# Inference
Wi = Train(objSeq,0.01,0.005,1000)
Pi = Wi@getFai(objSeq,objSeq)
print("objVec: {}, Wi: {}, P(x,y): {} ".format(objSeq,Wi,Pi))
if maxPi < Pi:
maxWi,maxPi,maxSeq = Wi,Pi,objSeq
print("The sequence with the highest probability is \n{}, Wi: {}, P(x,y): {} ".format(maxSeq,maxWi,maxPi))
5. result
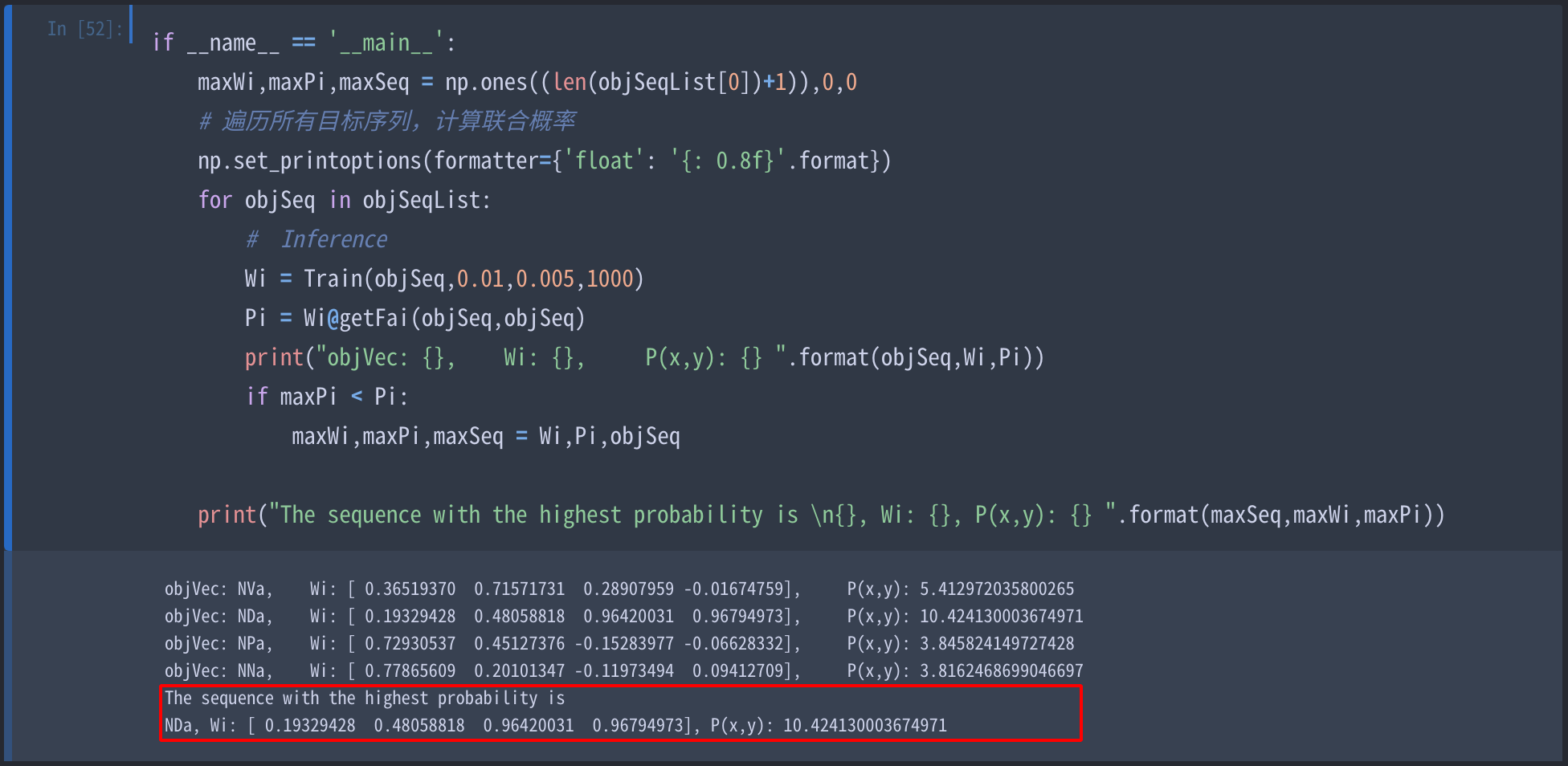
学习率eta = 0.01, 误差下界e = 0.005,训练 1000 次数得到的结果如下图,四个目标序列中,
NDa序列推断概率最大,因此推断结果为NDa
问题 & 改进
- 使用 Viterbi 算法优化。
- 对于这个小case,特殊化了特征集合,应该将构造的特征向量扩充到整个S集合和T集合。
